Altın Oranın Gizemi Matematik Doğa ve Sanatın Buluşması

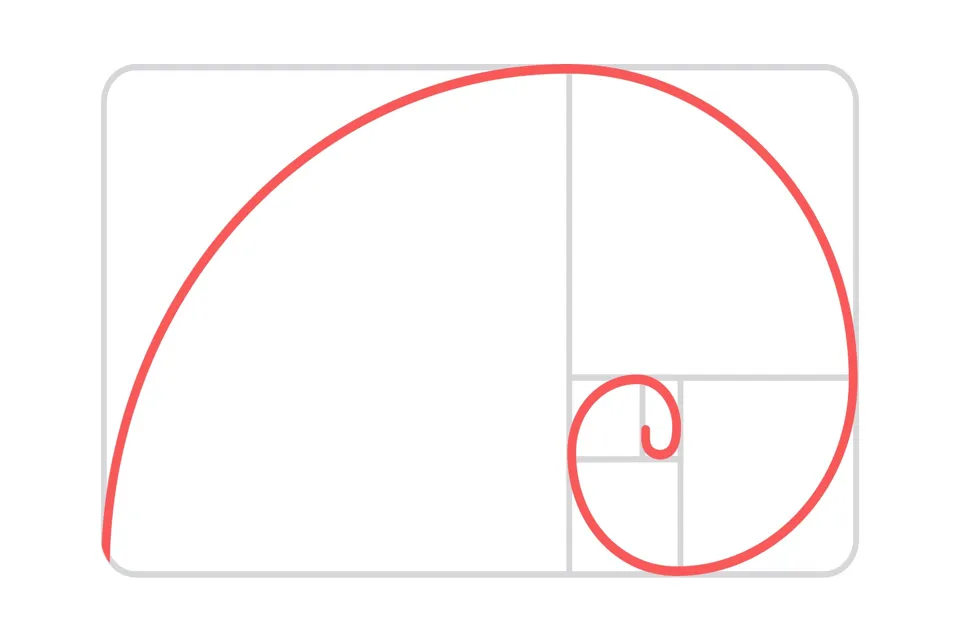
Soru: Hiç matematiğin ve doğanın en etkileyici sırlarından biri olan Altın Oran’ın hayatımıza nasıl dokunduğunu merak ettiniz mi? Bu bilinmezliğin ardında yatan mantık, zamanın ötesinde bir uyumun ve estetiğin anahtarını sunuyor. Tarih boyunca sanatçılar, mimarlar ve bilim insanları, evrenin mükemmel düzenini yansıtan bu oranın gizemini çözmek için çaba harcamışlardır.

Altın Oran, evrende, doğada ve insan yapımı eserlerde kendini tekrar eden bir orantı biçimidir. Çeşitli doğa olayları, galaksilerin spiral yapısı, deniz kabukları ve hatta insan vücudu, bu oranın etkileyici örneklerindendir. Matematikteki ifadesiyle, iki farklı büyüklüğün birbirine oranı, toplamlarına oranına eşitse, ortaya benzersiz bir denge çıkmaktadır işte bu orana Altın Oran denir.

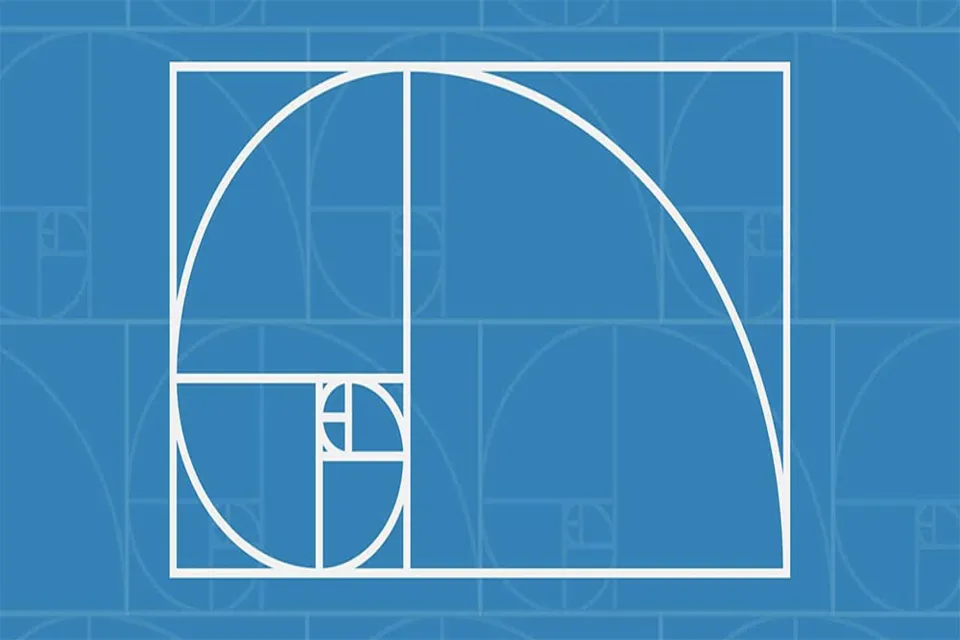
Gizemli ve büyüleyici olan bu oranın kökenleri, antik çağlara kadar uzanır. Eski Yunan'da, doğanın ve estetiğin hakiki temsilcisi olarak kabul edilen Altın Oran, mimarideki düzenlemelerden sanattaki kompozisyonlara kadar pek çok disiplinde uygulanmıştır. Bu oranın güzelliği, yalnızca sayıların ötesinde, insan zihninde estetik bir tatmin yaratmasıyla da kendini gösterir.

Tarih boyunca birçok ünlü isim ve kültür, bu olağanüstü oranın sırrını keşfetmek için uğraştı. Euclid ve Phidias gibi antik düşünürler, Altın Oran’ı matematiksel olarak tanımlamış, bunu sanatın ve mimarinin temeline yerleştirmişlerdir. Her birinin katkısı, Altın Oran’ın sadece bir matematiksel kavram olmadığını, aynı zamanda yaşamın kendine has düzeni ve uyumunun bir ifadesi olduğunu ortaya koymaktadır.

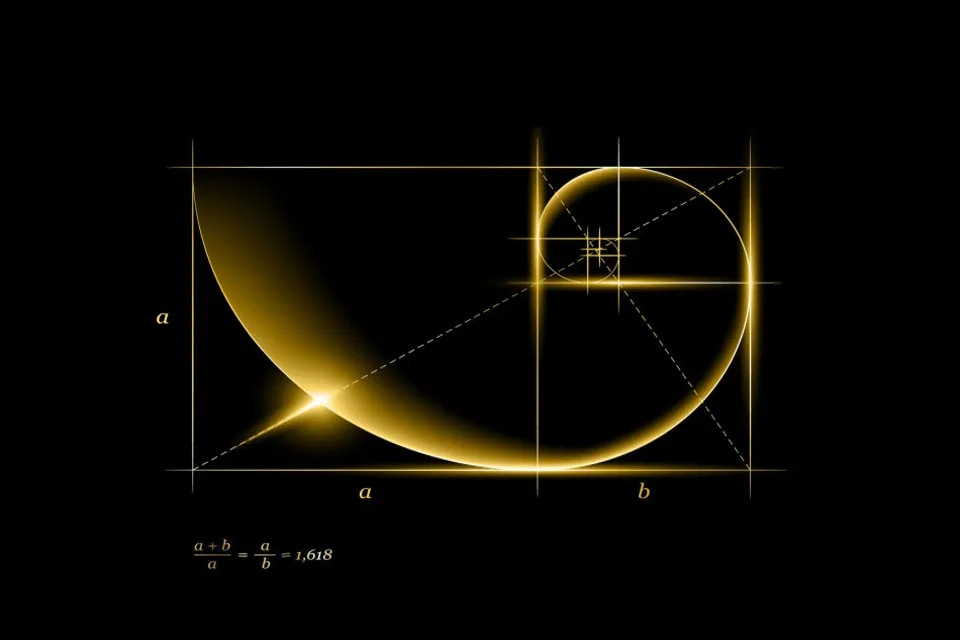
Modern dünyada, Altın Oran’ın etkileri bilim ve teknolojiden, grafik tasarım ve moda sektörlerine kadar geniş bir yelpazede kendini göstermektedir. Tasarımcılar, ürünlerinde bu oranın getirdiği estetik dengeyi kullanarak kullanıcı deneyimini zenginleştirmeyi amaç edinebilirken, mühendisler ise yapılarındaki dayanıklılığı ve simetrik düzeni korumak için ilham almaktadır. Bu durum, Altın Oran’ın evrenselliğini ve zamansız değerin altını çizmektedir.

Matematiksel formülüyle anlatıldığında, Altın Oran bir bütünün, parçalar arasındaki ilişkiyi öyle bir orantıyla düzenler ki, insan zihni burada sade bir sayısal değer yerine bir sanat eseri görür. Doğada kendine rastlanan bu düzenin gözlemlenmesi, doğanın özündeki mükemmel dengeleri anlamamıza yardımcı olmuş ve bunu birçok alanda yeniden yorumlamamızı sağlamıştır. Bu yönüyle Altın Oran, yalnızca teorik bir kavram değil, aynı zamanda pratik uygulamalarda da kendine yer bulmuş benzersiz bir araçtır.

Matematikseverler, sanatçılar ve bilim insanları arasında popülerliğini koruyan Altın Oran, aynı zamanda modern bilgisayar algoritmalarında ve veritabanı düzenlemelerinde de kullanılmaya başlanmıştır. Doğal formların matematiksel güzelliği, bilgisayar bilimlerinin estetik ve yapısal unsurlarında da görünür hale gelmiş böylece doğadan ilham alan algoritmalar geliştirilebilmiştir. Bu durum, insanlık tarihinin en eski matematiksel öğretilerinin bile günümüz teknolojisinin en ileri alanlarında yaşadığını göstermektedir.

Altın Oran’ın hayatımızdaki yeri, sadece yazılı ya da görsel sanatlarda değil, mimarinin ve tasarımın temel prensiplerinde de kendini gösterir. Pek çok ünlü yapı ve heykel, bu oranın etkileyici uyumunu yansıtarak göz alıcı ve dengeli kompozisyonlar oluşturmuştur. Yüzyıllardır insanların hayran kaldığı yapıtlar, Altın Oran’ın getirdiği simetrik ve doğayla uyumlu yapı sayesinde zamana meydan okur hale gelmiştir.

Bu eşsiz oranın arka planında yatan felsefi düşünce, evrenin karmaşık sistemi içinde basit ama derin bir düzenin var olduğunu öne sürer. İnsan aklının bu gizemi çözme çabası, Altın Oran’ın keşfiyle birlikte hem bilimsel hem de estetik anlayışımızın gelişmesine büyük katkı sağlamıştır. Böylece, yalnızca matematiksel bir oran olarak kalmayan Altın Oran, hayatımızdaki birçok alanda fark edilebilir bir estetik ve fonksiyonellik sunar.

Tüm bu etkileşimler, Altın Oran’ın neden bu denli önemli ve ilham verici bir kavram olduğunu gözler önüne serer. Doğanın kusursuz dengesinden, antik medeniyetlerin felsefi yaklaşımlarına modern tasarımların dikkatlice işlenmiş detaylarından, teknolojinin yenilikçi uygulamalarına kadar pek çok alanda Altın Oran izlenebilen bir ilham kaynağıdır. İnsan ruhunun derinliklerine hitap eden bu oran, bilim ve estetiğin kesişim noktasında durarak yaşamın her alanını etkiler hale gelmiştir.